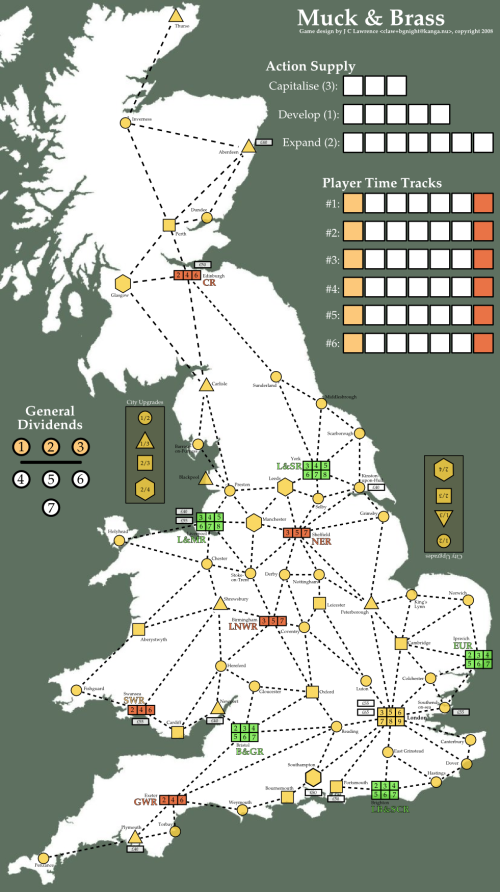
Ricochets toward stability
I haven’t gotten as much Muck & Brass played lately as I’d like, but I’m not complaining too hard given what else managed to hit the table (mostly a lot of 1889). That said and forgiven, I’m particularly pleased with how the new action selection method is working out in practice. The recent changes are two-fold:
- Action distribution changed to 3 Capitalise, 5 Develop, 7 Expand
- A Neuland/Thebes/etc-like combined action costing turn order mechanism is used to control turn order1.
The result is surprisingly dynamic. Wabash Cannonball has a fairly rote sequence of action selections in each round: 3 Capitalise followed by 5 Expand. Conversely Muck & Brass averages somewhere between 1 and 2 Capitalise actions per round with both 0 and 3 Capitalise actions in a round occuring if infrequently. The shift away from Capitalisation not only leads to increasingly cash-strapped companies but to a hurdy-gurdy pattern as the players struggle to balance short-term need with long-term viability. The patterns are delightful.
The core of the pattern is that a Capitalise early in the round takes so long (3 months) that it grants an enormous range of options and flexibility to the other players. Given the game’s blinding focus on liquidity, that’s simply unaffordable. The only players who seriously consider Capitalisation are the high-cash players who can be assured of winning the share. The result is that the early portion of rounds are dominated by Expands and Develops, the Develops usually being used to slip in an extra free action while catching up to a player earlier in the turn order. Then, as the end of the round approaches, usually it is the players early in the turn order who have the most control over when the round ends. They could Capitalise but their low cash position (which puts them early in the turn order) makes them unlikely to be able to win a share and none of the positions have developed enough to make alliance hunting/breaking viable – and in the meantime the Expand and Develop are both about to exhaust, ending the round anyway! Thus there’s great incentive to not Capitalise.
Which is fine and great until the companies start to run out of money. If a share isn’t capitalised those companies are dead ducks. This point usually hits either late in the second round or early in the third round, at which point there’s an added complexity. The fourth round is approaching, with its support for mergers, ports, double Expands, etc. The players are torn in multiple ways. They are still desperate for personal cash but they also want to start the next round with low cash (and high income) so as to have the positional control of early turn order, they have to get their companies Capitalised if they are to remain viable, and they have to build a tactical position to offer personally-advantageous ports-builds and mergers for when the fourth round starts. And just to make it worse, buying good shares will all too often earn such good dividends as to put the player late in the turn order! Arghh!
Then the fourth round starts, strong share-holders strive to merge their companies, accumulating their incomes and hopefully setting up a domino trail of mergers, weak share-holders build expensive ports to cripple their low-stake companies, leaving those companies prostrate to be merged into, hopefully by the companies they have larger holdings in. Meanwhile little tactical Expands, setting up honeypots and barriers for mergers and ports continues setting the scene. And again, companies are running out of money – except that now there are no shares left to sell to raise capital (only 3 per company)! Meanwhile the second round companies start to float, merging with the first round companies and injecting capital into their treasuries.
Often the game will end in the 5th or 6th round. It seems to only run until the 7th round if players have been really aggressive with the second round companies, blocking them out, building up their revenues and delaying the game while their income rate recovers their cash position. Certainly proper control and prediction of the second round companies can make the Wabash in Wabash Cannonball seem like a cakewalk.
It is all very delightfully tortured.
-
Actions are assigned costs in terms of time: Capitalise (3 months), Develop (1 month), Expand (2 months).. As players select actions their markers are moved forward on a track. The player that has spent the least time and started the round with the least cash has the current turn. Iterate until two players have used more than 5 months. ↩